MATEMATICA GENERAL: RACIONALIZACIÓN DE RADICALES

Para racionalizar un monomio de este tipo, se debe multiplicar el numerador y el denominador de la fracción por la raíz del denominador cuyo radicando se eleva a la diferencia entre el índice y el exponente. En el siguiente caso:

${\frac {{8}}{{\sqrt {5}}}}$

hay que multiplicar numerador y denominador por ${\sqrt {5}}$

${\frac {{8}}{{\sqrt {5}}}}\cdot {\frac {{\sqrt {5}}}{{\sqrt {5}}}}={\frac {{8{\sqrt {5}}}}{{\sqrt {5^{2}}}}}$

Después se despeja la raíz cuadrada del denominador ya que la cantidad subradical que es 5 elevada al cuadrado puede eliminar o despejar la raíz cuadrada:

${\frac {{8{\sqrt {5}}}}{{\sqrt {5^{2}}}}}={\frac {8{\sqrt {5}}}{5}}={\frac {8}{5}}{\sqrt {5}}$

También se debe tener en cuenta todas las propiedades para poder resolver los problemas de forma más fácil.

Se debe tener cuidado al realizar las operaciones entre los radicales, pues si se tiene

${\frac {{8}}{{\sqrt {x}}}}$

Al racionalizar que se debería dividir por

${\frac {{\sqrt {x}}}{{\sqrt {x}}}}$

es lo mismo

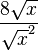${\frac {{8}{\sqrt {x}}}{{\sqrt {x^{2}}}}}$ que es correcto

que

${\frac {{8}{\sqrt {x}}}{{\sqrt {x}}^{2}}}$ que no correcto

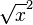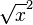Porque estaríamos ganando soluciones, es decir notemos que ${{\sqrt {x^{2}}}}$ (que seria el valor absoluto de un número) no es lo mismo que ${{\sqrt {x}}^{2}}$ ( que es el cuadrado de una raíz) entonces cuando ${x}$ sea un número negativo, la racionalización definiría una nueva solución, que no es correcto

Racionalización de binomio de índice 2

Para racionalizar un binomio de índice 2, se debe hacer un proceso similar al ejercicio anterior, multiplicar el numerador y denominador de la fracción por el conjugado del denominador de la misma. En el siguiente ejemplo:

${\frac {{2}}{{\sqrt {2}}+{\sqrt {3}}}}$

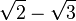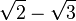hay que multiplicar el numerador y el denominador por ${{\sqrt {2}}-{\sqrt {3}}}$ ; este resultado es el que da el producto notable de los binomios conjugados.

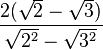
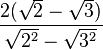${\frac {{2}}{{\sqrt {2}}+{\sqrt {3}}}}$ · ${\frac {{{{\sqrt {2}}-{\sqrt {3}}}}}{{\sqrt {2}}-{\sqrt {3}}}}$ = ${\frac {{2({{\sqrt {2}}-{\sqrt {3}}})}}{{\sqrt {2^{2}}}-{\sqrt {3^{2}}}}}$

${\frac {{2({{\sqrt {2}}-{\sqrt {3}}})}}{{\sqrt {2^{2}}}-{\sqrt {3^{2}}}}}$ = ${\frac {{2({{\sqrt {2}}-{\sqrt {3}}})}}{{2}-{3}}}$

${\frac {{2({{\sqrt {2}}-{\sqrt {3}}})}}{{-1}}}$ = ${-2({\sqrt {2}}-{\sqrt {3}}})$

El caso general de un binomio con dos raíces cuadradas también es fácilmente resoluble:

${\frac {1}{a{\sqrt {p}}+b{\sqrt {q}}}}={\frac {1}{a{\sqrt {p}}+b{\sqrt {q}}}}\cdot {\frac {b{\sqrt {q}}-a{\sqrt {p}}}{b{\sqrt {q}}-a{\sqrt {p}}}}={\frac {b{\sqrt {q}}-a{\sqrt {p}}}{b^{2}q-a^{2}p}}$

Más complicada es la racionalización de un trinomio:

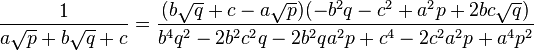
${\frac {1}{a{\sqrt {p}}+b{\sqrt {q}}+c}}={\frac {(b{\sqrt {q}}+c-a{\sqrt {p}})(-b^{2}q-c^{2}+a^{2}p+2bc{\sqrt {q}})}{b^{4}q^{2}-2b^{2}c^{2}q-2b^{2}qa^{2}p+c^{4}-2c^{2}a^{2}p+a^{4}p^{2}}}$

MATEMATICA GENERAL

domingo, 23 de febrero de 2014

RACIONALIZACIÓN DE RADICALES

Racionalización de binomio de índice 2

1 comentario: