Racionalización de un radical

Ecuación de primer grado

Ejemplo gráfico de ecuaciones lineales.

Una ecuación de primer grado o ecuación lineal significa que es un planteamiento de igualdad,

involucrando una o más variables a la primera potencia, que no contiene productos entre las

variables, es decir, una ecuación que involucra solamente sumas y restas de una variable

a la primera potencia. En todo anillo conmutativo pueden definirse ecuaciones de primer grado.

Solución de un Sistema de 2 x 2 por el Método de Sustitución

SISTEMA DE ECUACIÓN POR SUSTITUCIÓN

SISTEMA DE ECUACIÓN POR SUSTITUCIÓN 

http://www.youtube.com/watch?v=QfPGwU1Ora0

SISTEMA DE ECUACIÓN POR SUSTITUCIÓN

SISTEMA DE ECUACIÓN POR SUSTITUCIÓN 

http://www.youtube.com/watch?v=QfPGwU1Ora0

como racionalizar radicales

Racionalización de un radical

Para racionalizar un monomio de este tipo, se debe multiplicar el numerador y el denominador de la fracción por la raíz del denominador cuyo radicando se eleva a la diferencia entre el índice y el exponente. En el siguiente caso:

hay que multiplicar numerador y denominador por

Después se despeja la raíz cuadrada del denominador ya que la cantidad subradical que es 5 elevada al cuadrado puede eliminar o despejar la raíz cuadrada:

También se debe tener en cuenta todas las propiedades para poder resolver los problemas de forma más fácil.
Se debe tener cuidado al realizar las operaciones entre los radicales, pues si se tiene

Al racionalizar que se debería dividir por

es lo mismo

que es correcto

que

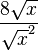que no correcto

Porque estaríamos ganando soluciones, es decir notemos que (que seria el valor absoluto de un número) no es lo mismo que 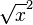( que es el cuadrado de una raíz) entonces cuando sea un número negativo, la racionalización definiría una nueva solución, que no es correcto

rasionalizacion

La racionalización de radicales es un proceso en donde se tiene que eliminar la raíz o raíces que están en el denominador de una fracción.
Racionalizar una fracción con raíces en el denominador, es encontrar otra expresión equivalente que no tenga raíces en el denominador. Para ello se multiplica el numerador y el denominador por una expresión adecuada, de forma que al operar, se elimine la raíz del denominador.

ejercicios de racionalizacion

Ejercicios resueltos de radicales